Shortly after the Nvidia announcement, Microsoft follows by adding DirectX Raytracing to the DirectX 12 api. According to the manufacturer, the technology clears the way for games that are partly built up via real-time raytracing and partly through traditional rasterization.
DXR will initially be used in games as an addition to existing rendering techniques such as screen space reflections , expects Microsoft;
Today, we are introducing a feature to DirectX 12 that will bridge the gap between the rasterization techniques employed by games today, and the full 3D effects of tomorrow. This feature is DirectX Raytracing. By allowing traversal of a full 3D representation of the game world, DirectX Raytracing allows current rendering techniques such as SSR to naturally and efficiently fill the gaps left by rasterization, and opens the door to an entirely new class of techniques that have never been achieved in a real-time game. Readers unfamiliar with rasterization and raytracing will find more information about the basics of these concepts in the appendix below.
What is DirectX Raytracing?
At the highest level, DirectX Raytracing (DXR) introduces four, new concepts to the DirectX 12 API:
- The acceleration structure is an object that represents a full 3D environment in a format optimal for traversal by the GPU. Represented as a two-level hierarchy, the structure affords both optimized ray traversal by the GPU, as well as efficient modification by the application for dynamic objects.
- A new command list method, DispatchRays, which is the starting point for tracing rays into the scene. This is how the game actually submits DXR workloads to the GPU.
- A set of new HLSL shader types including ray-generation, closest-hit, any-hit, and miss shaders. These specify what the DXR workload actually does computationally. When DispatchRays is called, the ray-generation shader runs. Using the new TraceRayintrinsic function in HLSL, the ray generation shader causes rays to be traced into the scene. Depending on where the ray goes in the scene, one of several hit or miss shaders may be invoked at the point of intersection. This allows a game to assign each object its own set of shaders and textures, resulting in a unique material.
- The raytracing pipeline state, a companion in spirit to today’s Graphics and Compute pipeline state objects, encapsulates the raytracing shaders and other state relevant to raytracing workloads.
You may have noticed that DXR does not introduce a new GPU engine to go alongside DX12’s existing Graphics and Compute engines. This is intentional – DXR workloads can be run on either of DX12’s existing engines. The primary reason for this is that, fundamentally, DXR is a compute-like workload. It does not require complex state such as output merger blend modes or input assembler vertex layouts. A secondary reason, however, is that representing DXR as a compute-like workload is aligned to what we see as the future of graphics, namely that hardware will be increasingly general-purpose, and eventually most fixed-function units will be replaced by HLSL code. The design of the raytracing pipeline state exemplifies this shift through its name and design in the API. With DX12, the traditional approach would have been to create a new CreateRaytracingPipelineState method. Instead, we decided to go with a much more generic and flexible CreateStateObject method. It is designed to be adaptable so that in addition to Raytracing, it can eventually be used to create Graphics and Compute pipeline states, as well as any future pipeline designs.
Anatomy of a DXR Frame
The first step in rendering any content using DXR is to build the acceleration structures, which operate in a two-level hierarchy. At the bottom level of the structure, the application specifies a set of geometries, essentially vertex and index buffers representing distinct objects in the world. At the top level of the structure, the application specifies a list of instance descriptions containing references to a particular geometry, and some additional per-instance data such as transformation matrices, that can be updated from frame to frame in ways similar to how games perform dynamic object updates today. Together, these allow for efficient traversal of multiple complex geometries.
The second step in using DXR is to create the raytracing pipeline state. Today, most games batch their draw calls together for efficiency, for example rendering all metallic objects first, and all plastic objects second. But because it’s impossible to predict exactly what material a particular ray will hit, batching like this isn’t possible with raytracing. Instead, the raytracing pipeline state allows specification of multiple sets of raytracing shaders and texture resources. Ultimately, this allows an application to specify, for example, that any ray intersections with object A should use shader P and texture X, while intersections with object B should use shader Q and texture Y. This allows applications to have ray intersections run the correct shader code with the correct textures for the materials they hit.
The third and final step in using DXR is to call DispatchRays, which invokes the ray generation shader. Within this shader, the application makes calls to the TraceRay intrinsic, which triggers traversal of the acceleration structure, and eventual execution of the appropriate hit or miss shader. In addition, TraceRay can also be called from within hit and miss shaders, allowing for ray recursion or “multi-bounce” effects.
Note that because the raytracing pipeline omits many of the fixed-function units of the graphics pipeline such as the input assembler and output merger, it is up to the application to specify how geometry is interpreted. Shaders are given the minimum set of attributes required to do this, namely the intersection point’s barycentric coordinates within the primitive. Ultimately, this flexibility is a significant benefit of DXR; the design allows for a huge variety of techniques without the overhead of mandating particular formats or constructs.
PIX for Windows Support Available on Day 1
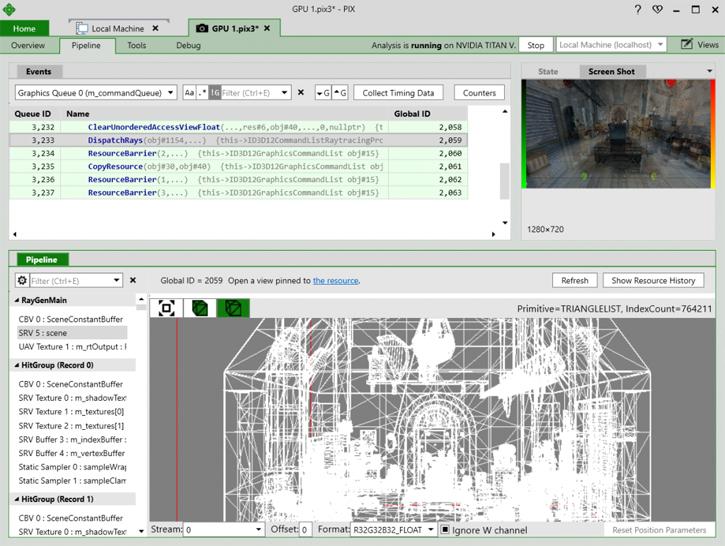
As new graphics features put an increasing array of options at the disposal of game developers, the need for great tools becomes increasingly important. The great news is that PIX for Windows will support the DirectX Raytracing API from day 1 of the API’s release. PIX on Windows supports capturing and analyzing frames built using DXR to help developers understand how DXR interacts with the hardware. Developers can inspect API calls, view pipeline resources that contribute to the raytracing work, see contents of state objects, and visualize acceleration structures. This provides the information developers need to build great experiences using DXR.
What Does This Mean for Games?
DXR will initially be used to supplement current rendering techniques such as screen space reflections, for example, to fill in data from geometry that’s either occluded or off-screen. This will lead to a material increase in visual quality for these effects in the near future. Over the next several years, however, we expect an increase in utilization of DXR for techniques that are simply impractical for rasterization, such as true global illumination. Eventually, raytracing may completely replace rasterization as the standard algorithm for rendering 3D scenes. That said, until everyone has a light-field display on their desk, rasterization will continue to be an excellent match for the common case of rendering content to a flat grid of square pixels, supplemented by raytracing for true 3D effects.
Thanks to our friends at SEED, Electronic Arts, we can show you a glimpse of what future gaming scenes could look like.
In addition, while today marks the first public announcement of DirectX Raytracing, we have been working closely with hardware vendors and industry developers for nearly a year to design and tune the API.
What Hardware Will DXR Run On?
Developers can use currently in-market hardware to get started on DirectX Raytracing. There is also a fallback layer which will allow developers to start experimenting with DirectX Raytracing that does not require any specific hardware support. For hardware roadmap support for DirectX Raytracing, please contact hardware vendors directly for further details.
Appendix – Primers on rasterization, raytracing and DirectX Raytracing
Intro to Rasterization
Of all the rendering algorithms out there, by far the most widely used is rasterization. Rasterization has been around since the 90s and has since become the dominant rendering technique in video games. This is with good reason: it’s incredibly efficient and can produce high levels of visual realism.
Rasterization is an algorithm that in a sense doesn’t do all its work in 3D. This is because rasterization has a step where 3D objects get projected onto your 2D monitor, before they are colored in. This work can be done efficiently by GPUs because it’s work that can be done in parallel: the work needed to color in one pixel on the 2D screen can be done independently of the work needed to color one the pixel next to it.
There’s a problem with this: in the real world the color of one object will have an impact on the objects around it, because of the complicated interplay of light. This means that developers must resort to a wide variety of clever techniques to simulate the visual effects that are normally caused by light scattering, reflecting and refracting off objects in the real world. The shadows, reflections and indirect lighting in games are made with these techniques.
Games rendered with rasterization can look and feel incredibly lifelike, because developers have gotten extremely good at making it look as if their worlds have light that acts in convincing way. Having said that, it takes an incredible deal of technical expertise to do this well and there’s also an upper limit to how realistic a rasterized game can get, since information about 3D objects gets lost every time they get projected onto your 2D screen.
Intro to Raytracing
Raytracing calculates the color of pixels by tracing the path of light that would have created it and simulates this ray of light’s interactions with objects in the virtual world. Raytracing therefore calculates what a pixel would look like if a virtual world had real light. The beauty of raytracing is that it preserves the 3D world and visual effects like shadows, reflections and indirect lighting are a natural consequence of the raytracing algorithm, not special effects.
Raytracing can be used to calculate the color of every single pixel on your screen, or it can be used for only some pixels, such as those on reflective surfaces.
How does it work?
A ray gets sent out for each pixel in question. The algorithm works out which object gets hit first by the ray and the exact point at which the ray hits the object. This point is called the first point of intersection and the algorithm does two things here: 1) it estimates the incoming light at the point of intersection and 2) combines this information about the incoming light with information about the object that was hit.
- To estimate what the incoming light looked like at the first point of intersection, the algorithm needs to consider where this light was reflected or refracted from.
- Specific information about each object is important because objects don’t all have the same properties: they absorb, reflect and refract light in different ways:
- different ways of absorption are what cause objects to have different colors (for example, a leaf is green because it absorbs all but green light)
- different rates of reflection are what cause some objects to give off mirror-like reflections and other objects to scatter rays in all directions
- different rates of refraction are what cause some objects (like water) to distort light more than other objects.
Often to estimate the incoming light at the first point of intersection, the algorithm must trace that light to a second point of intersection (because the light hitting an object might have been reflected off another object), or even further back.
Savvy readers with some programming knowledge might notice some edge cases here.
Sometimes light rays that get sent out never hit anything. Don’t worry, this is an edge case we can cover easily by measuring for how far a ray has travelled so that we can do additional work on rays that have travelled for too far.
The second edge case covers the opposite situation: light might bounce around so much that it’ll slow down the algorithm, or an infinite number of times, causing an infinite loop. The algorithm keeps track of how many times a ray gets traced after every step and gets terminated after a certain number of reflections. We can justify doing this because every object in the real world absorbs some light, even mirrors. This means that a light ray loses energy (becomes fainter) every time it’s reflected, until it becomes too faint to notice. So even if we could, tracing a ray an arbitrary number of times doesn’t make sense.
What is the state of raytracing today?
Raytracing a technique that’s been around for decades. It’s used quite often to do CGI in films and several games already use forms of raytracing. For example, developers might use offline raytracing to do things like pre-calculating the brightness of virtual objects before shipping their games.
No games currently use real-time raytracing, but we think that this will change soon: over the past few years, computer hardware has become more and more flexible: even with the same TFLOPs, a GPU can do more.
How does this fit into DirectX?
We believe that DirectX Raytracing will bring raytracing within reach of real-time use cases, since it comes with dedicated hardware acceleration and can be integrated seamlessly with existing DirectX 12 content.
This means that it’s now possible for developers to build games that use rasterization for some of its rendering and raytracing to be used for the rest. For example, developers can build a game where much of the content is generated with rasterization, but DirectX Raytracing calculates the shadows or reflections, helping out in areas where rasterization is lacking.
This is the power of DirectX Raytracing: it lets developers have their cake and eat it.